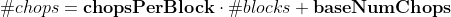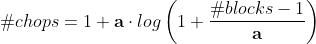For a more fun description, see CurseForge or Modrinth.
Let me know here!
Send me a log! See how to find and share Minecraft logs.
See the wiki - https://github.com/hammertater/treechop/wiki/Adding-compatibility-with-TreeChop
The number of chops required to fell a tree can depend on the size of the tree (the number of log blocks it contains), and is very configurable. Below, configuration options are highlighted like this and can be found in the /[your minecraft folder]/config/treechop-common.toml file after starting Minecraft with TreeChop installed at least once.
The algorithm used to determine the number of chops can be set to any of the options below, where each comes with its own set of parameters.
algorithm = "LINEAR"
The linear algorithm follows the function
where chopsPerBlock and baseNumChops are configurable and the actual number of chops required is rounded either UP, DOWN, or to the NEAREST whole number depending on the chopCountRounding configuration.
If chopsPerBlock > 1 or baseNumChops > 0, then you should consider the setting for canRequireMoreChopsThanBlocks, which determines whether the number of chops required to fell a tree can exceed the number of blocks in the tree. For example, setting baseNumChops = 8, chopsPerBlock = 0, and canRequireMoreChopsThanBlocks = true would mean that all trees fall after exactly 8 chops (the number of chops needed to whittle a single log block down to nothing).
algorithm = "LOGARITHMIC"
The logarithmic algorithm follows the function
where the parameter a is configurable and controls the steepness of the curve as the tree size (#blocks) increases.
The figure and tables below show how a affects the number of chops required for different tree sizes. The default value a = 10 results in the gray curve. At the extremes, if a = 0, then any size tree will only require one chop, and if a = ∞, then felling a tree will require the same amount of chops as there are blocks (the red curve).
The actual number of chops required depends on the rounding method (chopCountRounding), which may be DOWN, NEAREST, or UP.
| Number of blocks | 1 | 2 | 3 | 5 | 8 | 10 | 20 | 50 | 100 | 200 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Required chops (a = 1) | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 5 | 6 | 7 |
| Required chops (a = 10) | 1 | 1 | 2 | 4 | 6 | 7 | 11 | 18 | 24 | 31 | 47 |
| Required chops (a = 30) | 1 | 1 | 2 | 4 | 7 | 8 | 15 | 30 | 44 | 61 | 107 |
| Required chops (a = 80) | 1 | 1 | 2 | 4 | 7 | 9 | 18 | 39 | 65 | 100 | 209 |
| Required chops (a = ∞) | 1 | 2 | 3 | 5 | 8 | 10 | 20 | 50 | 100 | 200 | 1000 |
| Number of blocks | 1 | 2 | 3 | 5 | 8 | 10 | 20 | 50 | 100 | 200 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Required chops (a = 1) | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 5 | 6 | 6 | 8 |
| Required chops (a = 10) | 1 | 2 | 3 | 4 | 6 | 7 | 12 | 19 | 25 | 31 | 47 |
| Required chops (a = 30) | 1 | 2 | 3 | 5 | 7 | 9 | 16 | 30 | 45 | 62 | 107 |
| Required chops (a = 80) | 1 | 2 | 3 | 5 | 8 | 10 | 18 | 39 | 65 | 101 | 209 |
| Required chops (a = ∞) | 1 | 2 | 3 | 5 | 8 | 10 | 20 | 50 | 100 | 200 | 1000 |
| Number of blocks | 1 | 2 | 3 | 5 | 8 | 10 | 20 | 50 | 100 | 200 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Required chops (a = 1) | 1 | 2 | 3 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |
| Required chops (a = 10) | 1 | 2 | 3 | 5 | 7 | 8 | 12 | 19 | 25 | 32 | 48 |
| Required chops (a = 30) | 1 | 2 | 3 | 5 | 8 | 9 | 16 | 31 | 45 | 62 | 108 |
| Required chops (a = 80) | 1 | 2 | 3 | 5 | 8 | 10 | 19 | 40 | 66 | 101 | 210 |
| Required chops (a = ∞) | 1 | 2 | 3 | 5 | 8 | 10 | 20 | 50 | 100 | 200 | 1000 |